Sean is Coding #14: AI vs. Algorithms

Fun with AI quickly turned into fun with algorithms!

I’ve been spending a lot of time recently playing around with different AI APIs to better understand what they can and can’t do. (TheraGPT being one recent example that used OpenAI’s Chat Completions API with a Flask/Python backend.) 

One that’s getting a particularly high degree of attention is LangChain, a library that makes it easy to connect with other LLM providers’ (e.g. Anthropic, Cohere, GPT4All, etc.) APIs and even chain them together in a standardized way with integrations into vector-based DBs like Pinecone.

For this first test, I built a simple Tic-Tac-Toe game to see if the LLM would be smart enough to beat me in this strategically very simple game.

Sadly after a few dozen tests with both Open AI’s GPT 3.5-Turbo and Anthropic’s chat completions API, both models were failing miserably:

I did a bit of sleuthing and found a number of online discussions about ChatGPT’s deficiency when it comes to playing this simple game. Without going too deep, the reason why appears to have a lot to do with the activity LLMs are specifically trained to do: predict the next most logical word to follow a given set of words. Playing a game, even one as simple as Tic-Tac-Toe, is a fundamentally different activity.

While it was disappointing GPT wasn’t going to be suited to solve this particular problem, I was pretty excited to find that tic-tac-toe is a simple enough game that every possible move can actually fit nicely into a tree data structure.

Working with a tree like this is something that comes up often in technical interviews for engineering roles, but comparatively comes up far less often in the role itself (depending on your focus). As such, I like many aspiring professional engineers, have spent many evenings studying these data structures and strategies for traversing them efficiently. But I’ve always struggled with figuring out what a realistic, real-world application of this knowledge would look like.

It turned out that my struggle ended in one of the least likely places: a game of tic-tac-toe.

In the tree above, you have 9 possible board positions for the first move, eight for the second move, seven, and so on. So the overall number of combinations could be represented as 9! or 362,880 total possible nodes in a fully expanded tree. But this ignores the fact that the game is often over before all 9 squares are filled. So if you end each branch at the “terminal” move, you’re left with 26,830 total nodes, a completely manageable number for a computer to process.

So, what’s the best way to navigate this tree of possible Tic-Tac-Toe game states? Enter: the Minimax algorithm.

The Minimax algorithm is a recursive method used for decision making in game theory and artificial intelligence. The principle is simple: it's all about minimizing the worst-case scenario. In the context of Tic-Tac-Toe, this means that we assume that the opponent will always make their best possible move.

For every possible move, we play it out to the end (the "terminal" move), scoring the outcome. We give a high score if our AI wins, a low score if it loses, and a middling score if it's a draw. We then work our way back up the tree, choosing the highest (max) score if it's the AI's turn, and the lowest (min) if it's the opponent's. This is the "minimax" part of the algorithm.

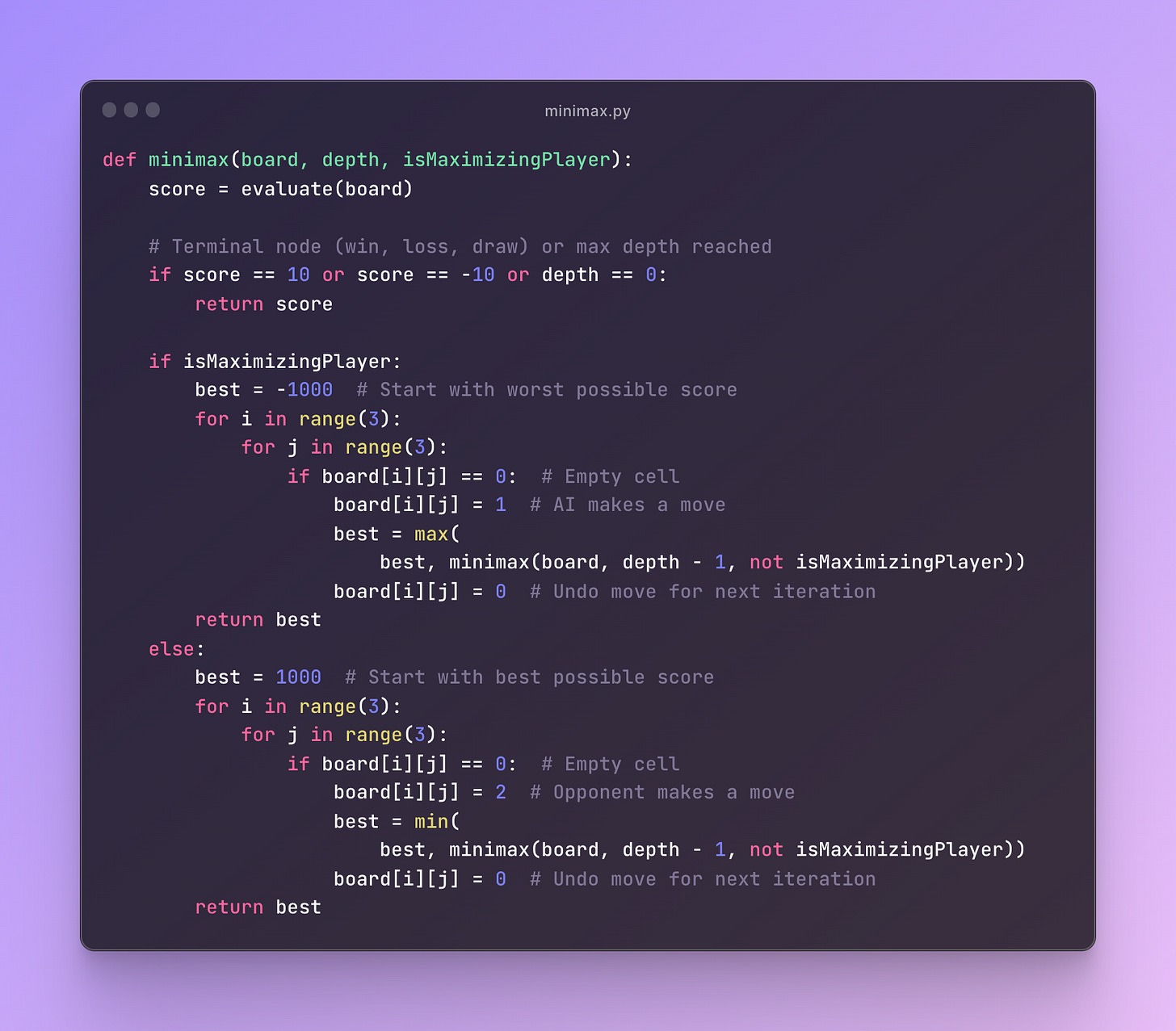
Let's illustrate this with some Python code:

Note: The evaluate(board) function in this snippet a separate part of the implementation that evaluates the current state of the board and returns a score.

Here, we're using a 3x3 matrix (list of lists in Python) to represent our Tic-Tac-Toe board. We assign a score of 10 to a winning move for the AI, -10 for a winning move for the opponent, and 0 for a draw or non-terminal move.

The isMaximizingPlayer parameter is a boolean that we flip at each depth level to represent whose turn it is. When it's the AI's turn, we want to maximize the score, and when it's the opponent's turn, we want to minimize the score.

The depth parameter is initially the number of empty cells and decreases as we make more moves. It's used as a simple way to stop the recursion when all cells are filled. 

This function recursively calls itself, playing out every possible game until it hits a terminal state or reaches maximum depth. It then evaluates the board, choosing the path that maximizes the AI's minimum gain.

To decide the AI's move, we'd simply call the minimax function for each possible move and choose the one that returns the highest score.

Originally, I was aiming to create an AI-enabled Tic-Tac-Toe champion. But as it turns out, programming and problem solving often leads you down paths you didn’t expect.

Instead of using AI, I found myself applying the Minimax algorithm, a concept I'd studied but hadn't yet gotten the chance to use in a real-world situation. Suddenly, those evenings spent studying trees and decision-making algorithms were paying off, and I actually started seeing “trees” of decisions and data in lots of places in my life (org charts, file systems, DOM trees, decision trees, etc. etc.).

So, even though I didn't end up where I initially thought I would, this one actually turned out to be a pretty great learning experience.

In conclusion, my friends, remember: Coding isn't always a straightforward path, but sometimes, those unexpected turns lead you to some pretty "tree-mendous" places. And even if you can't "branch" out with AI, don't worry, you can always "leaf" it to good old algorithms to save the day. After all, they're pretty unbe-leaf-able!

Until next time, keep exploring, keep learning, and remember to take the "root" less traveled - it might just lead you to a game of unbeatable Tic-Tac-Toe! Happy coding and keep "tree-ting" yourself to new coding adventures!

PS: Try your hand at the algo-enabled game here, and let me know if you win!